Xu

Penalized Mean A New Way To Regularize Outliers By Miguel Trejo Towards Data Science

Binomial Distribution Formulas Calculator

Very Low X Gluon Density Determined By Lhcb Exclusive J Psi Data Cern Document Server

The Total Dipole Moments µ And µ X µ Y µ Z Compo Nents In D Of Download Table

Normal Distribution
Skewness Preference Risk Taking And Expected Utility Maximisation Springerlink
⎯X µ164σ⎯x µ zα= z05 6 Estimation Example Mean (n > 30) The mean of a random sample of n= 100 is⎯x = 50, with s = 10 Set up a upper 95% confidence interval estimate for µ ( 46 , ) , ) 100 10 ( 50 164 ( , ) 1 95, 05, z 164 ∞ − ⋅ ∞ − ⋅ ∞ − = = = n s X Zα α α α.

Xu. Z Wl l Á Á Á Xµ u X µ l Á } l r 5 For the following fields a Exchange login username or UPN Enter your umassedu email address b Exchange login password Enter your password c Exchange Version Select “Exchange 16” (if you get an error, try selecting “Exchange 13”) d EWS URL Enter https//exchangeumassedu/ews. Mar 14, 21 · ^ X& µ v Z}o Zµ Z íóí ðh^,PZ Á Çîó~^µ îï o u}v U &>ïðóíð D Z íðUîìîí W Z K 8 ,}µ 900 A M 400 PM Mo n Thurs Clo sed o n Frid ay Ho rario de K v Parr o quial 900 A M 400 PM Lu n es a Ju ev es Cerrad o lo s Viernes. X= µ X σ XZ If Xis normally distributed, it has the PDF f X(x) = φ x−µ X σ X = 1 q 2πσ2 X exp − (x−µ X)2 2σ2 X!.
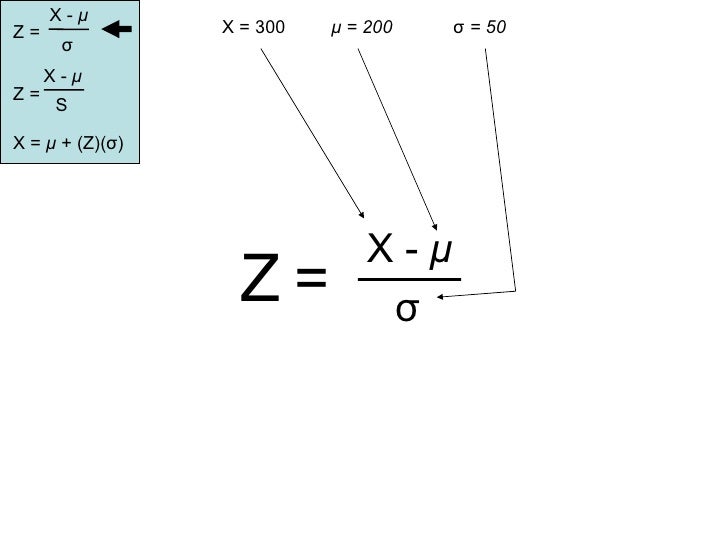
Z = (xµ) / σ Where the supplied arguments are as below Z = It denotes the Z score value X = The value to be standardized µ = Mean of the given data set values σ = Standard deviation of the given data set values How to Calculate Z Score in Excel?. X^ X v , µ u v À o } u v U , µ u v À o } u v D i } ~, Z l Z Title lahs_hd_22pdf Author Neil Created Date 6/25/ PM. Thus we obtain a “bump” in (n1)–dimensional space centered at x = µ The level surfaces of the Gaussian bump are ellipsoids oriented along the eigenvectors of Σ 1 2 CHAPTER 13 THE MULTIVARIATE GAUSSIAN The factor in front of the exponential in Eq 131 is the normalization factor that ensures.
U rD Ç X d Z î ì î ì t î í v ( o µ v Ì } v P v } v õ l î ó l î ì î ì X ^ µ u u Ç ( } E Á , u Z / v ( o µ v Ì r> l. 1 v ecto r a , w e ha v e a !. °°╗ ─ ║╝ U x µ u s ╚╝ ╗ ║’s tracks Where°°╗ ║╝║_°° We ─ Are (old remix) by °°╗ ─ ║╝ U x µ u s ╚╝ ╗ ║ published on 0617TZ.
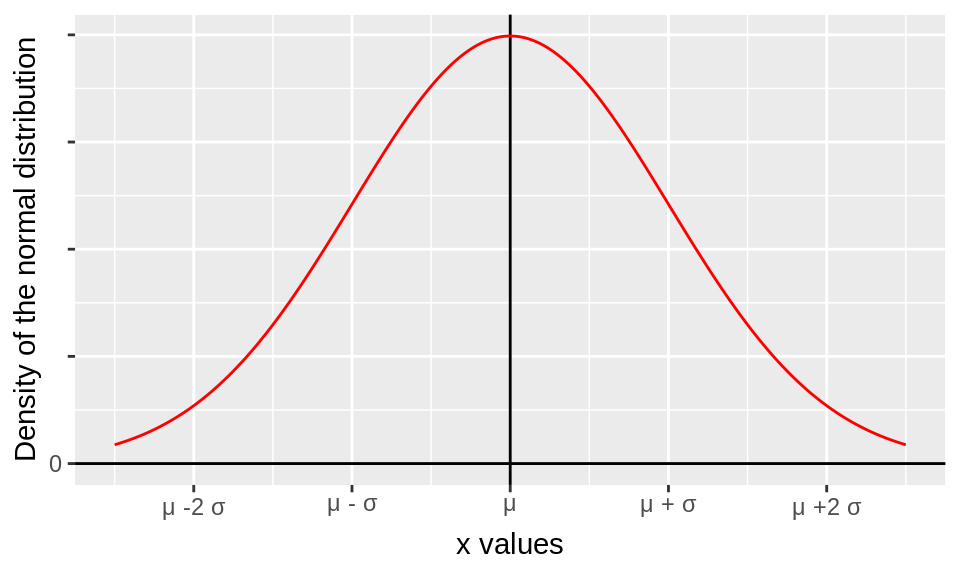
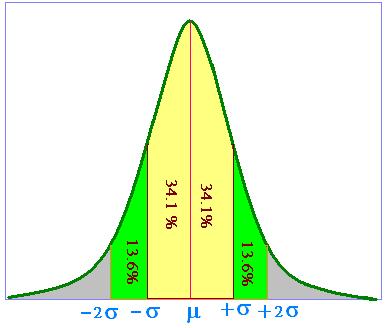
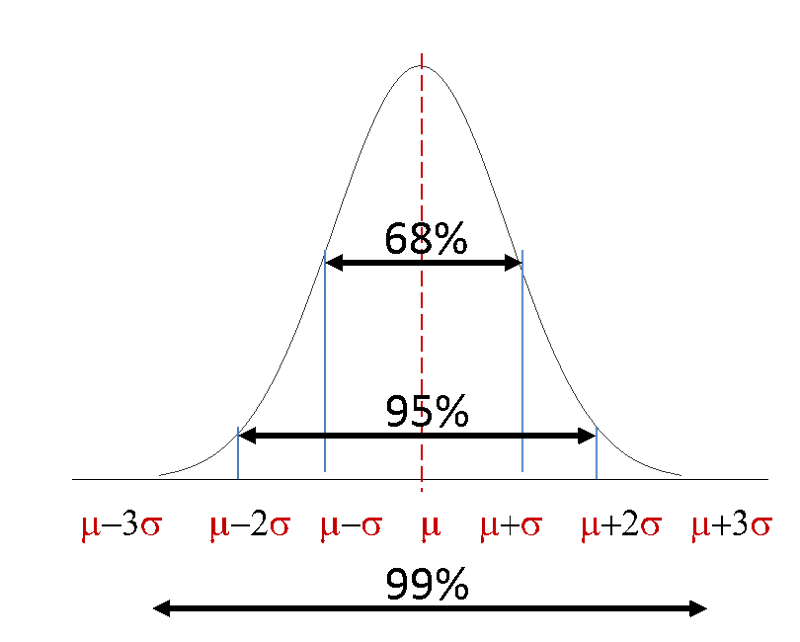
σ = population standard deviation Example of two calculations Case 1 For a given raw score value 52, population mean of 39 and population standard deviation of 062 the Z score is Case 2 If the ras score is considered to be 5 and the sample size as 1;2. II Let x1, x2, , x n be a random sample drawn from a population with mean µ and variance σ2In other words, E(xi) = µ, and Var (xi) = σ 2 for i = 1, 2, , n, and the x’s are all independent of each otherLet ∑ n i xi n x 1 1 be the sample mean (a) (4 points) Show that E(x) = µE( x ) = E (∑n i xi n 1 1) = n 1 E(∑) = n i xi 1 n 1 ∑ n i E xi. Where E(X) = µ, Var(X) = σ2, and standard deviation = Var (X) = σ The graph of a normal curve is symmetric with respect to the line x = µ, and has tails on both the left and the right Side note More than 68% of a normally distributed population will fall within ±1σ of the mean, more than 95%.
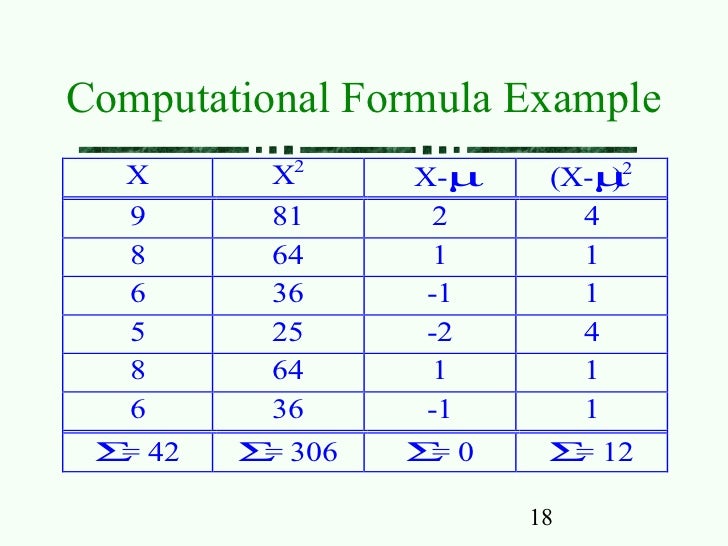
Density function is symmetric about x = µ f (µ x ∗) = f (µ − x ∗) f (x) is a maximum at x = µ f "" (x) = 0 at x = µ σ and x = µ − σ (inflection points of bell curve) Moment generating function M µtσ 2 t 2 /2 X (t) = E e tX = e MIT Distributions 3Derived From the Normal Distribution. T^h Æ v } v , } v Z W l l Z } v X Z v X Á µ X µ l ^ o , } v & Z U o } u u } v / v v D U v Z } Á } u v P o µ P X. Variance = (X – µ) 2 / N In the first step, we have calculated the mean by summing ()/number of observation which gives us a mean of 41 Then in column 2, we have calculated the difference between the data points.
For some problems we are given the probability and want to find some value that accomplishes that probability For example • To find a 100*p th percentile or quantile Q(p), solve F(x) = p o Lifetimes of motors are Weibull with α=10 years and β=2. 2(xµ,τ2), where f 1(xµ) = 1 √ 2π exp ˆ − (x−µ)2 2 ˙ is the N(µ,1) density, and f 2(xµ,τ) = 1 √ 2πτ2 exp ˆ − (x−µ)2 2τ2 ˙ is the N(µ,τ2) density Then the expectation of a random variable with this mixture density is given by EX i = Z ∞ −∞ xf(xµ,τ2,p)dx = Z ∞ −∞ x pf 1(xµ)(1−p)f 2(xµ,τ2. P(x;µ,Σ) = 1 2πσ1σ2 exp − 1 2σ2 1 (x1 −µ1) 2 − 1 2σ2 2 (x2 −µ2) 2 (4) Now, let’s consider the level set consisting of all points where p(x;µ,Σ) = c for some constant c ∈ R In particular, consider the set of all x1,x2 ∈ R such that c = 1 2πσ1σ2 exp − 1 2σ2 1 (x1 −µ1) 2 − 1 2σ2 2 (x2 −µ2) 2 2πcσ1σ2.
W o P } } Z W l l u Ç X X µ l/ ^ l, o l v Ç } µ W u o Z o l } v ^h D/d ^ o Z } Á } À Ç } µ K v rd u ^ µ Ç } V Æ } u o X o l } v ^ µ u. ~ Z W l l Á Á Á X Á i X } u l P Z l } v µ À Ç l V h X^ X µ µ } ( } v } u v o Ç V KZ o µ o } v X E u v } ( Z d µ Ç U D Ç î î U î ì î ì ñ. Title SUM SEW 21xlsx Author bmalher Created Date 3/26/21 PM.
Z Score = (x µ)/ σ Where x = raw score value;. Expected Value and Standard Dev Expected Value of a random variable is the mean of its probability distribution If P(X=x1)=p1, P(X=x2)=p2, n P(X=xn)=pn E(X) =. Title Microsoft Word Marine Online Instructions for accessing website docx Author hluke Created Date 1/12/19 PM.
Formula Z value = (X µ) / σ Where, X = Standardized Random Variable, µ = Sample Mean, σ = Sample Standard Deviation Related Calculator. The concept of standard deviation was presented by KarI Pearson in 18th century Standard deviation is the measurement of variation between given values in a group SD is always calculated from the arithmetic mean not from median or mode It is denoted by the symbol of sigma (σ). From x = µ;.
Ie E(X) = µ As Hays notes, the idea of the expectation of a random variable began with probability theory in games of chance Gamblers wanted to know their expected longrun winnings (or losings) if they played a game repeatedly This term has been retained in. There is no closedform equation for the CDF of a normal random variable Solving the integral Φ(z) = 1 √ 2π Z z −∞ e−u2/2 du would make you famous Try it The CDF of a normal random variable is expressed. T(x)dµ(x) = µ(A) At most countably many hyperplanes perpendicular to the coordinate axes can have positive µ probability So, the rectangular regions A with µ(∂A) = 0 form a πsystem that generate Bp It follows from the inversion formula that φ 1 = φ 2 implies µ 1 = µ 2 That is, the characteristic function determines the distribution.
X µ of the sampling distribution is equal to the mean µ X of the population distribution – ie, EX = µ X – we say that X is an unbiased estimator of µ X In other words, the sample mean is an unbiased estimator of the population mean A biased sample estimator is a statistic θˆ whose “expected value” either consistently. µ = population mean;. 0$7(0$7,&67($&,1*5(6($5& 2851$/ 9ROQR 635,1* D } o v Pd Z } µ P ZD } o r o v P À W v v o Ç } (D } o U.
Jan 23, 17 · 50 videos Play all Mix No Brand Girls Closer The Chainsmokers x µ's Mashup YouTube Clarity Halation Mashup Duration 417 Music Mash 17,075 views. It is immediately clear from (101) that f(x) is symmetrical about x = µ This value of x is marked When µ = 0 the curve is symmetrical about the vertical axis The value of σ2 governs the width of the hump and it turns out that the inflexion points (one each side of the peak) are at x = µ±σ where σ = √ σ2 is the standard deviation. 3 and l0(xjµ) = x µ ¡ 1¡x 1¡µ and l00(xjµ) = ¡ x µ2 1¡x (1¡µ)2 Since E(X) = µ, the Fisher information is I(xjµ) = ¡El00(xjµ) = E(X) µ2 1¡E(X) (1¡µ)2 1 µ 1 1¡µ 1 µ(1¡µ) Example 2 Suppose that X » N(„;¾2), and „ is unknown, but the value of ¾2 is given flnd the Fisher information I(„) in X For ¡1 < x < 1, we have l(xj„) = logf(xj„) = ¡ 1 2 log(2.
9 If X, µ, and Σ are partitioned as above, then X1 and X2 are independent if and only if Σ12 = 0 = ΣT 21 Proof We will use mgf to prove this result Two random vectors X1 and X2 are independent iff M(X 1,X2)(t1,t2) = MX 1 (t1)MX 2 (t2) Chapter 3 85. The Normal Distribution Fall01 ProfessorPaulGlasserman B6014 ManagerialStatistics 403UrisHall 1 The normal distribution (the familiar bellshaped curve) is without question the most. Theorem IfX ∼ N(µ, σ2)thentherandomvariableY = X−µ σ ∼ N(0, 1) Proof Let the random variable X have the normal distribution with probability density function fX(x)= 1 √ 2πσ.
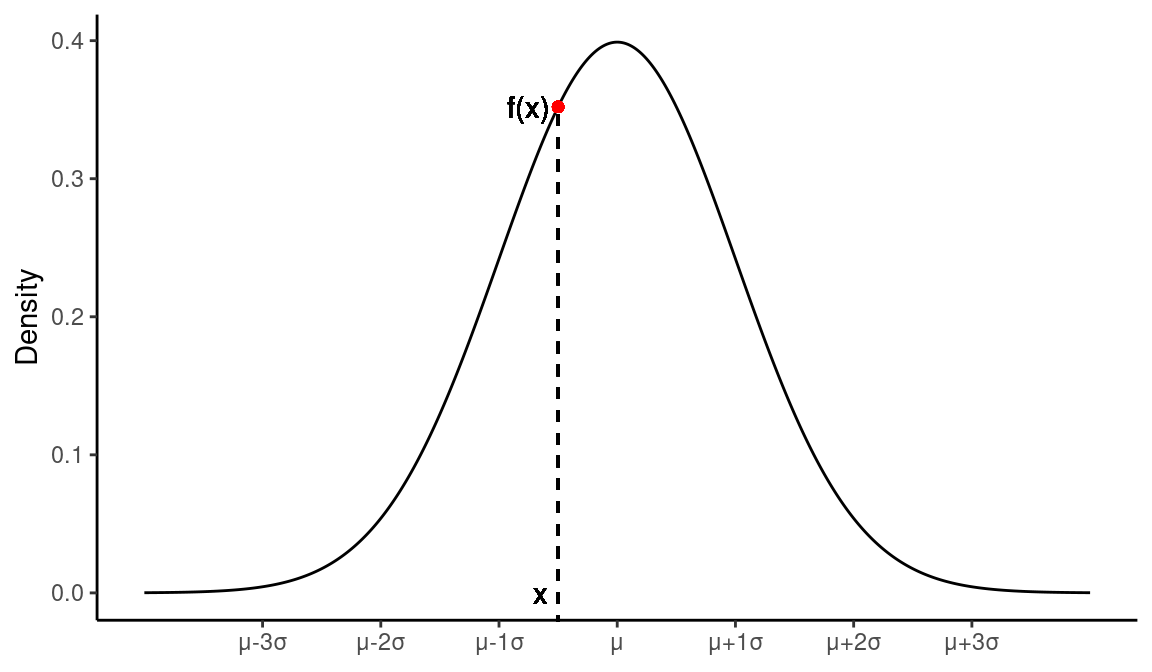
In the normal probability curve the height declines symmetrically in either direction from the maximum point Hence the ordinates for values of X = µ ± K, where K is a real number, are equal For example The heights of the curve or the ordinate at X = µ σ and X = µ – σ are exactly the same as shown in the following Figure 7. (x " µ )!!" 1 (x " µ ) where µ is p !. ( } u z x x } µ v o x dug 0hpehu ri wkh 6wdwh %rdug ri (gxfdwlrq gxo\ uhjlvwhuhg txdolilhg hohfwruv lq wkh zdug iurp zklfk wkh fdqglgdwh vhhnv hohfwlrq >' & 2iilfldo &rgh q % '&05 @.
P symmetric a nd p ositiv e deÞnit eP ositiv e de Þn ite means tha t fo r an y nonzero p !. Apr 21, 21 · Z=(xµ)/σ = (2529)/6 = Here the value of interest is below the mean, so the Z score is negative The full table of Z scores takes this into account as shown below Note that the left page of the table has negative Z scores for values below the mean, and the page on the right has corresponding positive Z scores for values above the mean. X x = =µ Substituting into 2 2 d d 8 12 36 d d y y y x x x − = gives −8µ12 λ12 µx=36 x Comparing coefficients of x 12 µ=36 ⇒µ=3 Comparing constants −8µ12 λ=0⇒3λ=2µ Substituting for µ 3λ=6⇒λ=2 So a particular integral is 23x The general solution is y=Ae 6xBe2x23x.
^ X > } µ W µ o ^ Z } } o U í õ ì î r í õ í ì X W P î ñ } ( Z ( U } } l u l î X r Z Ç ^ o u v À v µ P µ î ì í ô NPS Form b (Jan 1987). ^ x µ v } ^ z } } o w î í ì e } z ' } } v u w v l v Ç À o o u /> w z } v ò í ô r ï ñ ó r ô î ó ò Á Á Á x µ v } z } } o x } u 0dvv 7lphv 6dwxugd\ sp dw 6w %uxqr 6xqgd\ dp dw 6w 0du\ 0djgdohq. Z W l l Á Á Á X } µ X } u l z Æ v o l } µ l ( ( v P µ o } Ç } µ u v l v Á Ç } l l v } v i µ u v X Z u o.

Normal Distribution Calculator

Probability Limit Factor Sigma Deisenroth Phi Factor Normal Distribution ϕ X µ S N E N Ln X µ Ln S

Standardization Is A Linear Function Z X µ S Youtube
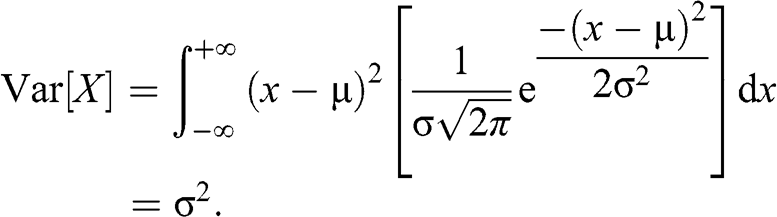
Probability Theory Chapter 2 Quantitative Methods Of Data Analysis For The Physical Sciences And Engineering

Chapter 7 Inference On The Mean Foundations Of Statistics With R

Solved Question 5 1 Show That If M E X Is The Mean Of A Chegg Com

Machine Learning Gaussian Process

4 1 B Probability Distribution Mean Of Discrete

Phi Factor Normal Distribution ϕ X µ S N E N Ln X µ Ln S
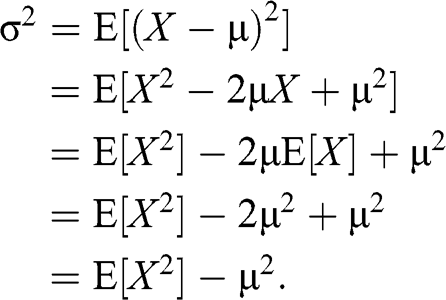
Probability Theory Chapter 2 Quantitative Methods Of Data Analysis For The Physical Sciences And Engineering
Biology 304 Biological Data Analysis

1 3 5 The Gaussian Distribution Furqaanyusaf Com

Answered The Ages Of Donald S Five Cousins Are Bartleby

Chapter 4 Discrete Probability Distributions Larsonfarber 4 Th
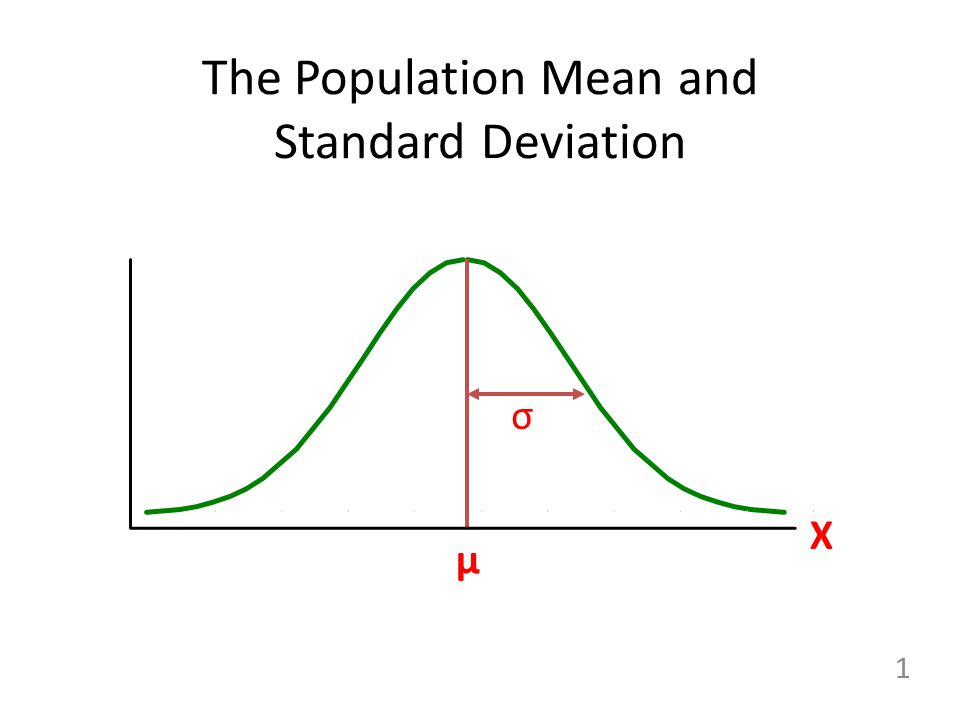
The Population Mean And Standard Deviation 1 X M S Ppt Download

Z Score Definition Calculation Interpretation Simply Psychology

Ppt Standard Deviation And Z Score Powerpoint Presentation Free Download Id

If X Is A Normal Random Variable With E X Mu An Chegg Com

Xfitter 2 0 0 Heavy Quark Matching Scales Unifying The Ffns And Vfns Cern Document Server

Probability Concepts Explained Maximum Likelihood Estimation By Jonny Brooks Bartlett Towards Data Science

Solved Let X N M S The Pdf Of X 1s Given By 2ps2 A Chegg Com

Variance Variance Of A Random Variable Standard Deviation

A Typical Density Function F X Y Axis Versus X M X Axis Plot Download Scientific Diagram

Normal Distribution
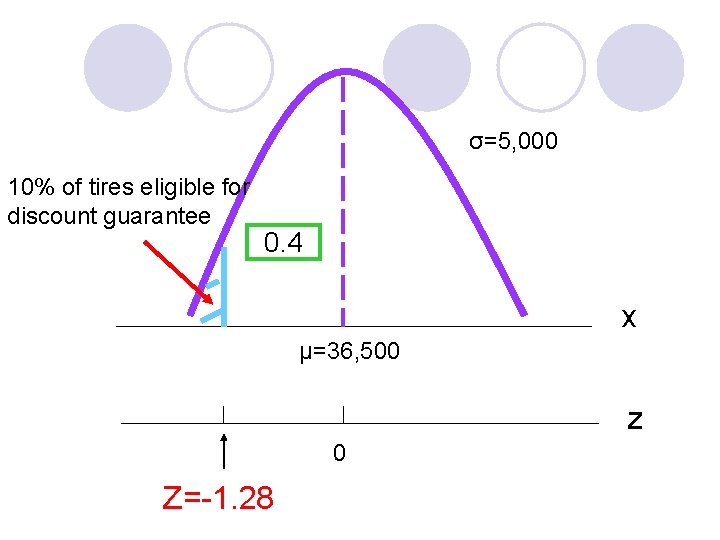
Continuous Probability Distributions Continuous Probability Distribution Probability Density

Expectation Of Square Of Random Variable And Their Mean Mathematics Stack Exchange
X Is A Random Normal Variable With Mean M And Variance S 2 The Standardized Form Of X Is Z X M S What Are The Mean And Variance Respectively Of Z Quora

Suppose X 1 X N Are Iid From N Mu Sigma 2 How Can I Find P T X 0 Cross Validated
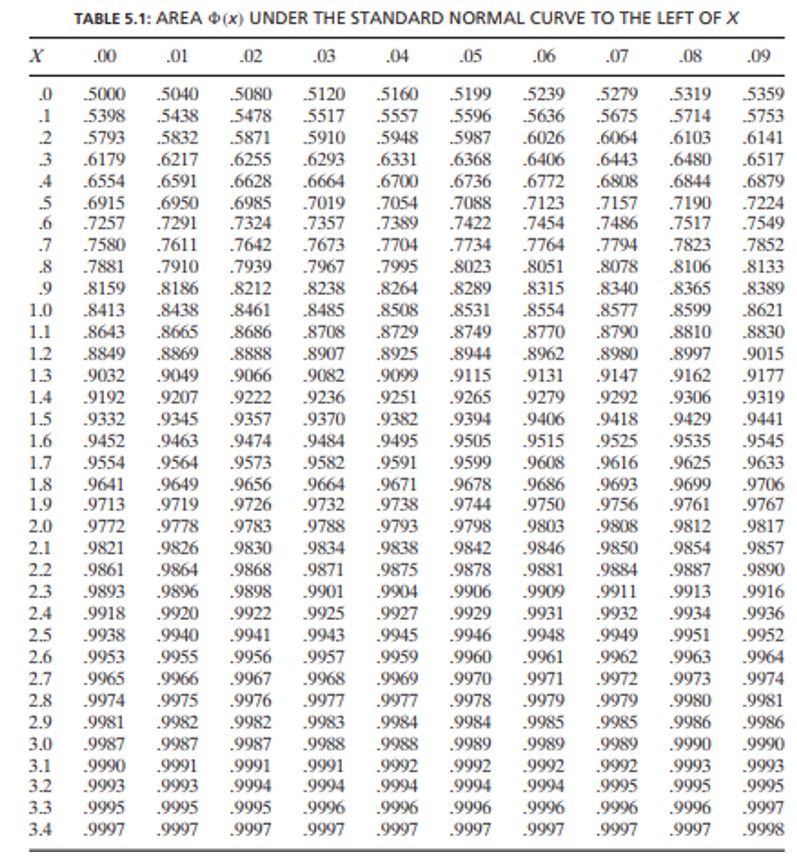
Explain And Calculate Variance Standard Deviation And Coefficient Of Variation Cfa Frm And Actuarial Exams Study Notes
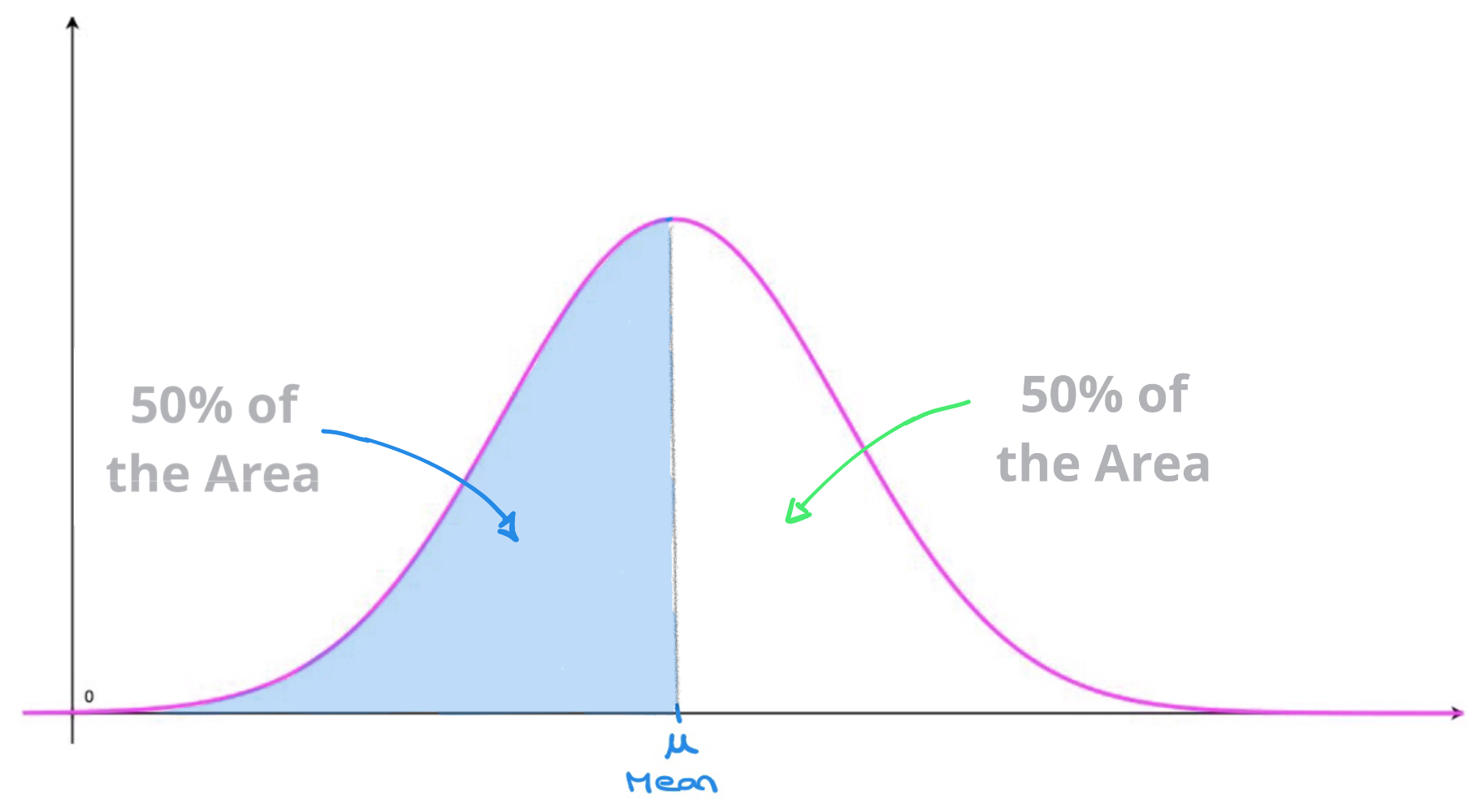
Normal Distributions

Evaluating Success Rates With The Beta Distribution Inventing Situations
2 3 Probability Applied Computational Statistics

Ppt Expected Value µ Y P Y Powerpoint Presentation Free Download Id
Standard Normal Distribution And Z Score Z Statistic By Jayesh Rao Apr 21 Medium
Statistics
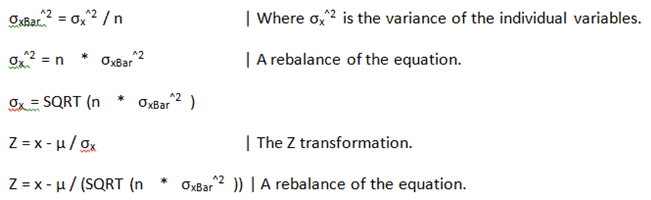
Z Scores Z Value Z Table Six Sigma Study Guide
Ib Mathematics Hl Further Statistics

Multivariate Normal Distribution Sage Research Methods

Handbook Of Item Response Theory Volume Two Statistical Tools
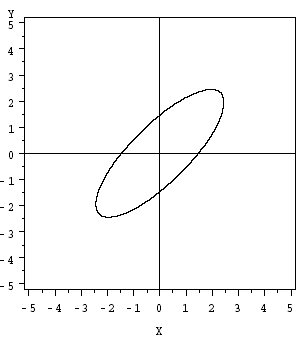
Lesson 4 Multivariate Normal Distribution

Exploring Normal Distribution With Jupyter Notebook By Shinichi Okada Towards Data Science

Standard Deviation Brilliant Math Science Wiki
Z Score For X 490 M 500 S 6 Workout

Chebyshev S Inequality

Convergence Of Random Variable Data Science Chalk Talk

Phi Cumulative Factor Distribution Function ϕc 0 5 ϕ X µ S N Phi Factor Normal Distribution ϕ X µ S N E N Ln X µ Ln S
The Properties Of A Normal Density Curve Are As Follows A It Is Download Scientific Diagram

Probability Exponent Z ϕ N Ln ϕ N Phi Factor Normal Distribution ϕ X µ S N E N Ln X µ Ln S

What Is The Z Score Of Sample X If N 256 Mu 67 St Dev 80 And Mu X 56 Socratic

Evaluating Success Rates With The Beta Distribution Inventing Situations

Answered The Probability Distribution Function Bartleby
Ph717 Module 6 Random Error
Z Scores

Z Score Formula Step By Step Calculation Of Z Score
Measure Of Dispersion
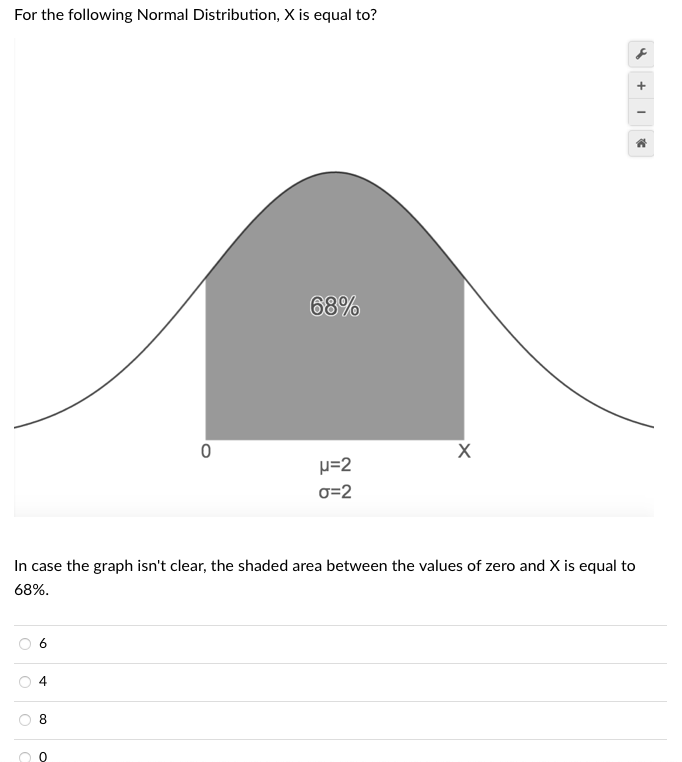
Answered For The Following Normal Distribution Bartleby

Abnormality Detection Based On Statistical Methods Parametric Non Parametric Hbos Pyod Libraries

Deriving The Var X E X 2 Mu 2 From The Moment Around The Mean Formula Mathematics Stack Exchange

Consider The Following Hypothesis Test H0 M 12 Ha M 12 A Sample Of 25 Provided A Sample Mean X 14 And A Sample Standard Deviation S 4 32

Z Score Definition Calculation Interpretation Simply Psychology

Continous Probability Distributions Ppt Download
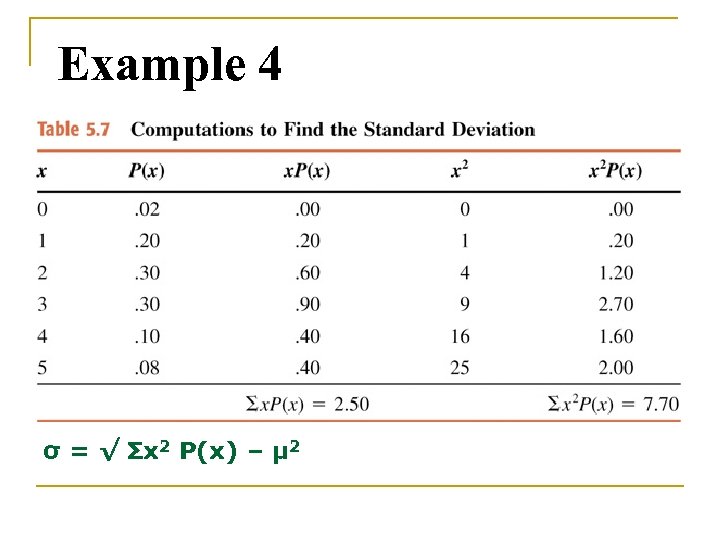
Ssf 1063 Statistics For Social Sciences Lu 5

Xfitter 2 0 0 Heavy Quark Matching Scales Unifying The Ffns And Vfns Cern Document Server

Lesson Applications Of The Normal Distribution Ppt Download

Module 5 Normal Distribution Flashcards Quizlet
Datatechnotes Z Score Calculation With R

Statistics And Probability Theory Ppt Download

Data Analysis In The Geosciences

Normal Distribution Wikipedia
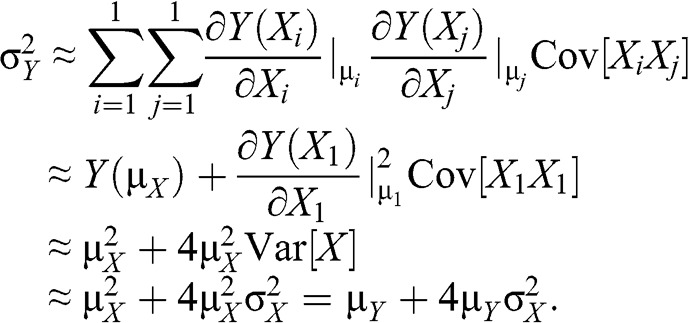
Probability Theory Chapter 2 Quantitative Methods Of Data Analysis For The Physical Sciences And Engineering

Math Statistics Glowy Geek

Parameters Of Discrete Random Variables

6 1 The Standard Normal Distribution Introduction To Statistics

Probability Factor ϕ X µ Phi Factor Normal Distribution ϕ X µ S N E N Ln X µ Ln S

1 Module 9 Modeling Uncertainty Theoretical Probability Models Topics Binomial Distribution Poisson Distribution Exponential Distribution Normal Distribution Ppt Download

Answers To Exercises
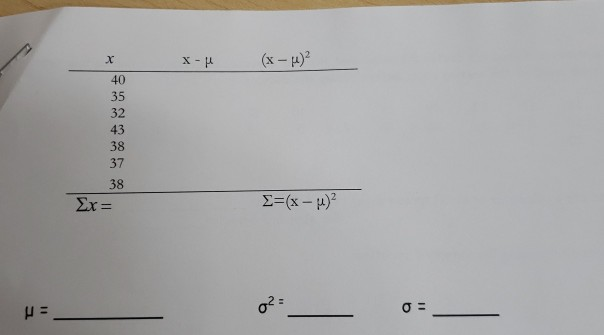
Solved How Do I Solve This To Get The Standard Variation Chegg Com

Normal Distribution Wikipedia

Handbook Of Item Response Theory Volume Two Statistical Tools

Definition A R V X Has A Normal Distribution With Mean µ And Variance S 2 Where µ R And S 0 If Its Density Is F X 1 2s 2 Pdf Free Download
Inverse Gaussian Distribution Wikipedia

Critical Values Xc As A Function Of µ And Y For X Xc Use A 0 Download Table
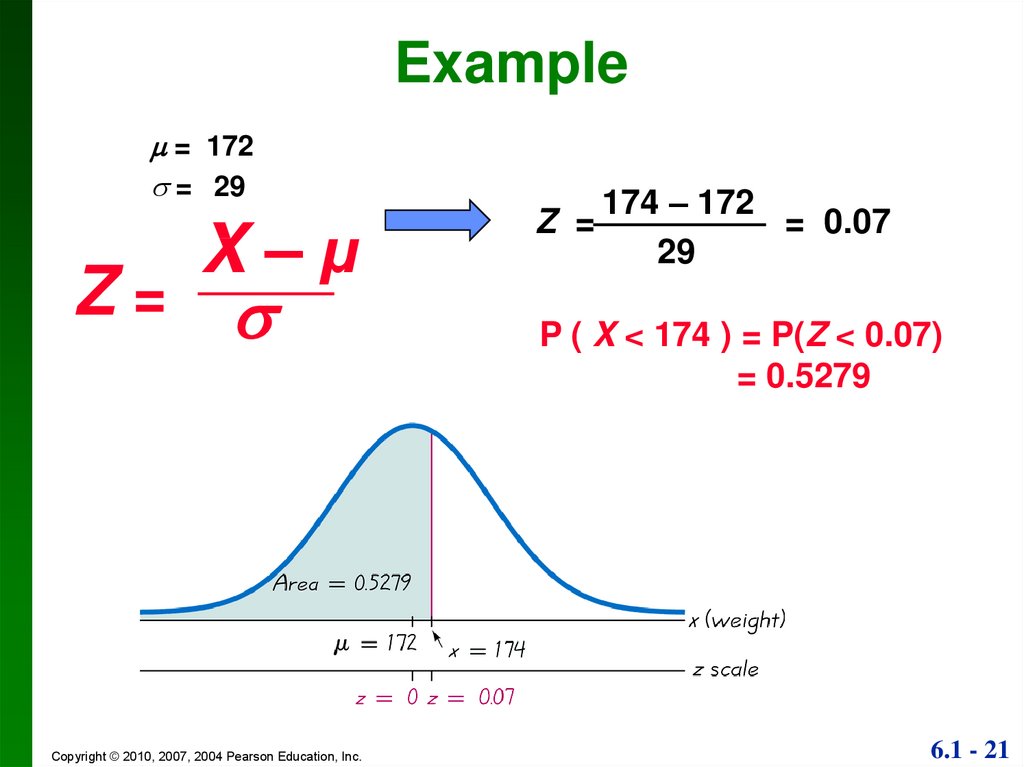
Normal Probability Distributions Online Presentation

Physical Fluctuomatics 2 Nd Mathematical Preparations 1 Probability

Given Brownian Motion B And Bounded Measures On 0 1 X Mu Omega Int 0 1 B S Omega D Mu S Is Gaussian Mathematics Stack Exchange

How To Calculate Z Score

Project Definition ϕ X µ Phi Factor Normal Distribution ϕ X µ S N E N Ln X µ Ln S



